Rationale and performances of a data-driven method for computing the duration of pharmacological prescriptions using secondary data sources – Scientific Reports
Simulated data
Simulated data were used to evaluate the performance of correctly computing the duration of filled prescriptions and determine the exposure status of the SEE method. Via simulations, the true duration of exposure to a pharmacological treatment and exposure status were generated and then compared with those computed with the SEE method15. In a pharmacoepidemiologic setting, it is crucial to simulate data on filled prescriptions that resemble patterns observed in the real world. To mimic the real world, these patterns should include different gradients of re-filling intensity of prescriptions ranging from individuals that refill frequently their medication to those that rarely or never re-fill their prescriptions. Different gradients of re-filling intensity of prescriptions are well captured in summary measures of intensity of medication use in an observational window, e.g. adherence. The simulation was performed by adapting the R functions and procedures described by Allemann and colleagues16. One single dataset was simulated containing filled prescription histories of a pharmacological treatment for 1000 patients restricted to an initially filled prescription of 30days and at least one subsequent filled prescription over an observational window of 2years. According to the simulation performed by Allemann and colleagues, fixed prescription durations of 1, 2, or 3months were generated randomly for each subsequent prescription following six adherence trajectories that have been previously observed in real-world data of patients treated with antihypertensive medications (Fig.2)17,18. The six adherence trajectories were used to create six groups mimicking real-world treatment patterns for which adherence was (1) high (95%), (2) medium (5090%), (3) gradually declining over time, or (4) intermittent (with a change between high and low adherence at regular intervals). Additionally, (5) Partial drop-off (with high adherence initially and partial drop-off after some time) and (6) non-persistence (with one or two refills after the initial fill and no refills afterward) trajectories were simulated16. In this simulation, carry-over within and before the observational window was not performed. This approach assumes that all previous filled treatment was consumed before starting the next filled prescription.
Real-world data
The SEE was also tested in real-world data using selected pharmacological treatments with widely used therapeutic drug monitoring in Denmark. Real-world data were retrieved from Danish administrative registers, including the civil registration system (socio-demographic characteristics)19, the register for medicinal product statistics (prescription fillings in pharmacies)20, the register of causes of death (date/cause of deaths)21, the national patient register (hospital admissions/ambulatory visits)22, and the register for laboratory results for research (biomarkers and therapeutic drug monitoring results)23. These registers have high validity and have previously been used in several pharmacoepidemiologic studies24. The linkage between Danish registers is possible since each Danish citizen has a personal identification number which is used as a key of linkage after pseudonymization. The selection included 19 drugs consisting of 11 antiseizure medications (carbamazepine, valproate, phenobarbital, gabapentin, lamotrigine, pregabalin, topiramate, zonisamide, levetiracetam, clobazam, and clonazepam), 5 antidepressant drugs (amitriptyline, citalopram, clomipramine, mirtazapine, and nortriptyline), 2 antiarrhythmic drugs (propafenone and flecainide), and 1 bronchodilator (theophylline). The choice of focusing on these drugs is driven by the analytical strategy in which dates of measurements of plasma concentrations obtained through irregular therapeutic drug monitoring were used to determine the true exposure status to pharmacological treatments. In the real-world data, there was no information about the length of filled prescriptions and exposure status in the observational window. Therefore, detectable plasma concentrations of medications were used as a proxy of true exposure status. This means that if the patients had a measurable plasma concentration they were considered exposed on that day or relatively close to the date of the plasma measurement (based on the half-life of the drug). To include similar dosing schemes, for antiseizure medications and antidepressants, the analyses were restricted to individuals with a diagnosis of epilepsy (International Classification of Diseases 10th revision,ICD10code G40) and depression (ICD10 codes F32 and F33), respectively. Since theophylline, propafenone, and flecainide do not have a different dosing scheme for different indications of use, the preliminary selection of individuals with a pre-specified diagnosis was not made. The study population was composed of individuals that filled their first prescription of the selected drugs and divided into 19 cohorts, one for each drug under investigation. Each individual could contribute to one or more cohorts. The date of the first filled prescription of the drug under investigation was the start of follow-up and will be denoted further in the text as the index date. The study population was followed from the index date to the end of data coverage in 2018. Individuals with detectable plasma concentrations were considered exposed and this was regarded as the real exposure status based on the assumption that a patient with a detectable plasma concentration was recently exposed to the medication (Fig.1).
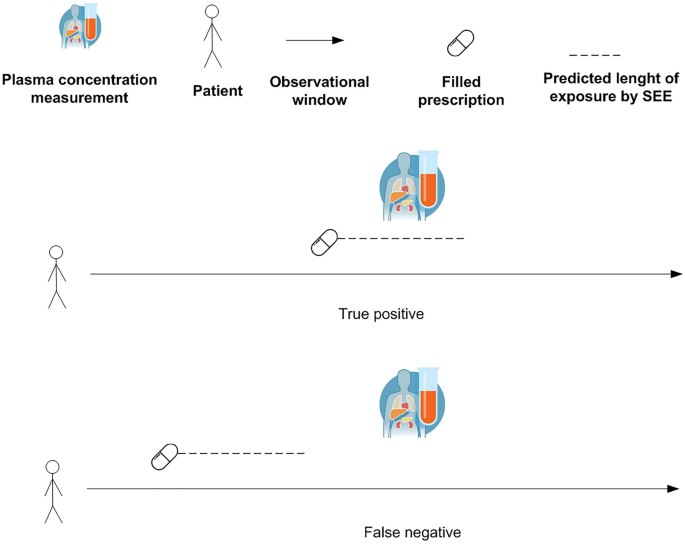
Evaluation of true positives and false negatives in real-world data. SEE = Sessa Empirical Estimator.
Sessa empirical estimator (SEE)
The SEE is an algorithm composed of multiple steps aiming to compute the duration of filled prescriptions when information regarding the true duration is not available. The method relies on the availability of individual-level information on the date of filling of a medicinal product for computing the duration of filled prescriptions. It assumes that the duration of a filled prescription is associated with the temporal distance between subsequently filled prescriptions as previously described in the WTD method7,8,11. Moreover, it is assumed that the amount dispensed is consumed by the patient during the time between two filled prescriptions. The method aims at clustering temporal distances between filled prescriptions into K groups with similar filled prescription patterns and then assigns durations of filled prescriptions within each of the K groups.
The algorithm steps and rationales are described in the following:
-
1.
Among dates of filling of consecutive prescriptions of all patients within the observational window, the SEE computes the Empirical Cumulative Distribution Functions (ECDF) of temporal distances. To avoid including artificially long temporal distances introduced by early- and delayed-discontinuers, the method retains only 80% of the ECDF.
Rationale Artificially long temporal distances can be generated by using the temporal distance between two subsequent filled prescriptions due to, for example, individuals that stop and re-start treatments (stoppers and re-starters), individuals with poor adherence, individuals with missing information on treatments administered during hospitalizations, etc. Stoppers and re-starters are individuals that start medication at one point in time and stop (e.g., due to an adverse reaction to the pharmacological treatment) for a long period before starting the medication again. This problem is solved by cutting the last 20% of the ECDF, which includes the very long temporal distances among consecutive prescriptions.
-
2.
For each individual in the study population, the SEE randomly selects a pair of consecutive filled prescriptions in the observational window.
Rationale By selecting only a random pair of consecutive filled prescriptions, the method removes the overrepresentation of individuals which fill prescriptions of the pharmacological treatment more often due to a lower amount prescribed. If all the prescriptions would be included those individuals would contribute more to the estimation of the median temporal distances than those filling prescriptions less often due to a higher amount prescribed.
-
3.
The temporal distances for the randomly selected filled prescriptions undergo standardization25. Subsequently, using the K-means algorithm, the temporal distances are clustered intoKgroups minimizing the sum of squares from the temporal distances to the assigned cluster centers26, and the optimal number of clusters is selected using Silhouette Analysis27.
Rationale The temporal distances are standardized by calculating the temporal distances vectors mean and standard deviation, then each element is scaled by removing the mean and dividing by the standard deviation.
The standardized vector of temporal distances is used for clustering using the K-means algorithm. Standardization is performed since K-means is a distance-based algorithm that is affected by the scale of a variable28. Silhouette Analysis provides the optimal number of clusters measuring the quality of the clustering and it is used to determine how well each object lies within its cluster. A high average silhouette width indicates good clustering. Therefore, the method selects the number of clusters to be used in the K-means clustering algorithm providing the highest value of the average silhouette widths.
-
4.
For each cluster, the SEE builds the probability density function (PDF) of temporal distances to find the median temporal distance. These median values are used as the computed duration of the prescriptions in the cluster.
Rationale This step is performed to obtain the computed durations of filled prescriptions for each cluster (the median temporal distance).
-
5.
Finally, the SEE computes the end of supply for each filled prescription using the computed durations.
Rationale Based on the computed durations of filled prescriptions the end of each supply is computed as the date of filling plus the computed duration.
Analysis of simulated data
For descriptive purposes, a density plot showing the six adherence trajectories simulated is presented (Fig.2). For each individual in the study population, a random date in the observational window was selected. The true versus the SEE assessed exposure status was compared. To evaluate the performances of the method, a confusion matrix29 was obtained for the random dates from which accuracy, sensitivity, specificity, positive and negative computed values (PPV/NPV), balanced accuracy, kappa, F1, recall, and precision in assessing exposure status were computed. The classification of individuals in the confusion matrix is reported in Table 1.
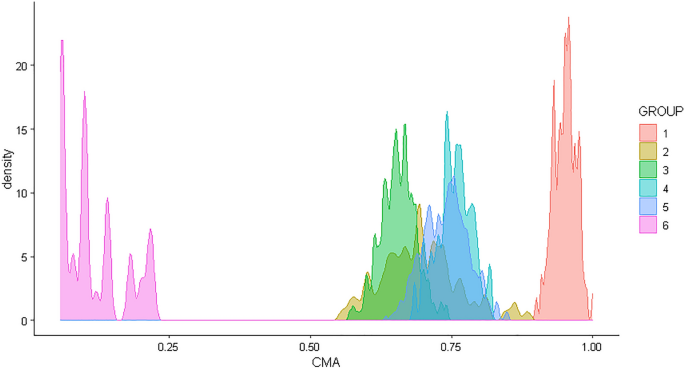
Density plot of adherence for the six groups mimicking real-world treatment patterns for which adherence was 1) high (95%), 2) medium (5090%), 3) gradually declining over time, or 4) intermittent (with a change between high and low adherence at regular intervals), 5) Partial drop-off (with high adherence initially and partial drop-off after some time), and 6) non-persistence (with one or two refills after the initial fill and no refills afterward) (see also Allemann and colleagues16). CMA = Continuous multiple interval measures of medication availability.
To account for unbalanced groups in the confusion matrix, a sensitivity analysis was performed using a random sample of individuals that were true positives. Finally, to calculate the number of days of misclassification of exposure status, the duration computed by the SEE was compared with the true duration of each filled prescription. Moreover, the absolute value of the difference between the true duration of each filled prescription versus the duration computed by the SEE was computed separately for true positives, false positives, true negatives, and false negatives.
Analysis of real-world data
For each cohort, median age and interquartile range (at the index date), the proportion of female sex, and the proportion of individuals filling their first prescription in 1995 (when the register of medicinal product statistics started) were tabulated and presented separately for individuals with and without plasma concentration measurements. Among individuals with measurements of plasma concentration of the drug under investigation, the true versus the SEE assessed exposure status was compared and sensitivity was assessed. Individuals were considered truly exposed to the medication at the date of measurement/s if they had a detectable plasma concentration of the medication. To assess if the median duration of different filled prescriptions (e.g., 1st, 2nd, 3rd, 4th, etc.) for each cohort was similar during the observational window, boxplots of the temporal distances between consecutive prescriptions were presented. The analysis has been presented separately for individuals with and without measurements to show their comparability in terms of medication use over time. With the final goal of comparing the performances of the SEE, sensitivity was assessed also for an RDD method widely used in the scientific literature which uses the assumption of a treatment consumption equal to the fixed amount of one unit per day (Supplementary Table 1 reports the dosage recommendations in the Danish Summary of Product Characteristic (SmPC) for the 19 drugs under investigation). The comparison between the proposed method and the RDD method has been presented as a bar chart of sensitivity.
Software used for data analysis
Simulations and data analyses were performed using R 4.0.0 (R Core Team, 2020). Reporting and design of simulations were performed according to relevant guidelines for simulation of data in medical statistics30. An R package implementing the SEE is currently available on GitHub (https://github.com/arkh88/SEE_test) and a Shiny app is available online (https://sessaempiricalestimator.shinyapps.io/SessaEmpiricalEstimator/).